題目
題目
給予一組數字陣列長度為n,用來表示海拔高度,詢問在雨後可以累積多少水量.
解題思路
先將題目給的測資簡化,n 最小可以為1,設想當海拔高度只有一個時,並不會形成坑洞可以積水,所以累積水量為0。
那有兩個海拔高度的時候,e.g. [1 , 0 , 1],則如下圖。

範例1
無論右邊的高度如何只要不為0,累積水量=min(左邊海拔高度,右邊海拔高度) * 右邊海拔位置 - 左邊海拔位置?
以這個例子來說是 min(1,1) * 2 - 0 - 1,之所以 -1 是因為實際存水的是中間空格位置。
似乎只要 for loop 每個海拔位置,並且跟下一個海拔位置比較就好?
Pseudocode-1
初始化answer = 0
初始化left = 0,用來表示左邊海拔高度位置
從第1個海拔位置開始,遍歷海拔高度:
如果遍歷到的位置的海拔大於0:
answer += min(左邊海拔高度,遍歷到的海拔高度) * 遍歷到的海拔高度 - 左邊海拔高度 - 1
更新左邊海拔高度=遍歷到的海拔高度
但是這個方法沒有考慮到中間有其他海拔高度,當中間有其他海拔就不能成立。
看看下個範例,[2,0,1,0,2]

範例2
這時轉換思考,是否當左邊最高海拔高度 >= 最右邊海拔高度的時候,可以利用左邊最高海拔高度減去中間所有的海拔高度得到累積水量?
Pseudocode-2
初始化answer = 0
初始化max_left = 0,用來表示左邊最高海拔高度位置
從第1個海拔位置開始,遍歷海拔高度:
#遍歷每個海拔的時候更新左邊最高高度
max_left= max(max_left,遍歷到的海拔高度)
answer += max_left - 遍歷海拔高度
但這算法依然有問題,只有當最右邊的海拔高度是從右邊看來最高的才成立。
範例,[3,0,1,0,3,0,2]
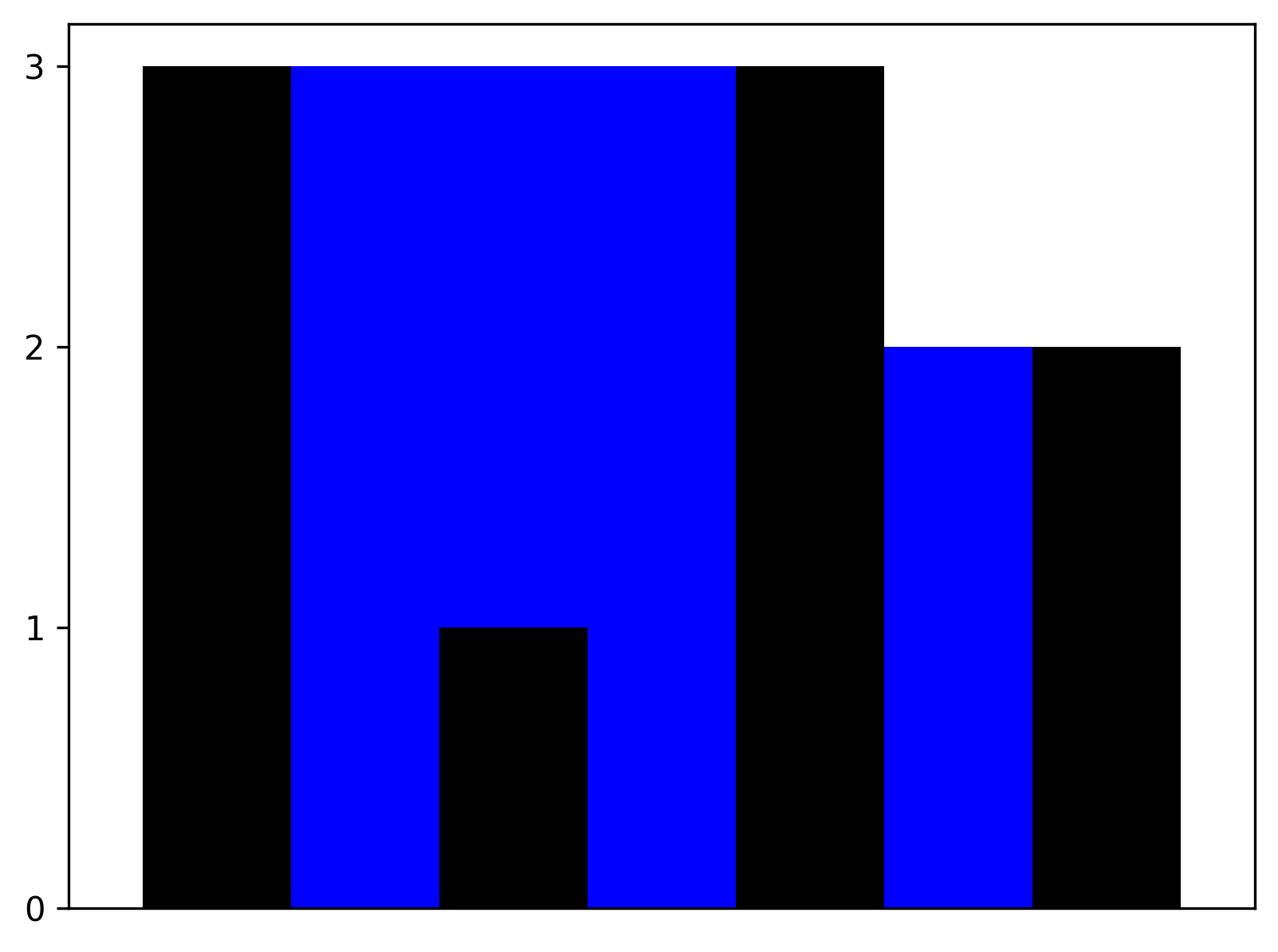
範例3
這時思考是否不該只從左邊迴圈看過來更新左邊最高海拔高度,也需要從右邊海拔高度看過來?
但是什麼條件下該移動左邊什麼時候該移動右邊呢?
先以左邊來思考,右邊海拔高度必須 >= 左邊海拔高度,才能用左邊海拔高度減去遍歷的高度。
使用 max_left= max(max_left,遍歷到的海拔高度),直接來更新左邊最高高度有以下目的:
- 當遍歷的高度比左邊最高海拔高度低的時候,不會更新,answer += max_left - 遍歷海拔高度,便可以累積水量。
- 當遍歷的高度比左邊最高海拔高度高的時候,更新了,max_left - 遍歷海拔高度 = 0,當先前的最高高度比遍歷的高度低的時候,也不能累積水量。
Pseudocode-3
初始化answer = 0
初始化max_left = 0,用來表示左邊最高海拔高度位置
初始化max_right = n - 1,用來表示右邊最高海拔高度位置
從第1個海拔位置開始,遍歷海拔高度:
如果 max_right >= max_left:
max_left= max(max_left,遍歷到的海拔高度)
answer += max_left - 遍歷海拔高度
但這裡又有個問題,該怎麼更新右邊的最高海拔高度?
轉換想法,以兩個變數分別指向左邊跟右邊海拔位置,從左右開始往中間移動,來遍歷海拔高度。
Pseudocode-4
初始化answer = 0
初始化left = 0 ,用來表示左邊目前遍歷的海拔位置
初始化right = n - 1,用來表示右邊目前遍歷的海拔位置
初始化max_left = 海拔高度[0],用來表示左邊最高海拔高度位置
初始化max_right = 海拔高度[n - 1],用來表示右邊最高海拔高度位置
當 left < right:
如果 max_right >= max_left:
left + 1 右移到下一個位置
max_left = max(max_left,left位置的海拔高度)
answer += max_left - left位置的海拔高度
否則:
right - 1 左移到下一個位置
max_right = max(max_right,right位置的海拔高度)
但在這個方法中依然會漏掉倒數第2個海拔高度位置的水量。
所以從右邊左移的時候也應該要計算累積水量。
Pseudocode-5
初始化answer = 0
初始化left = 0 ,用來表示左邊目前遍歷的海拔位置
初始化right = n - 1 ,用來表示右邊目前遍歷的海拔位置
初始化max_left = 海拔高度[0],用來表示左邊最高海拔高度位置
初始化max_right = 海拔高度[n - 1],用來表示右邊最高海拔高度位置
當 left < right:
如果 max_right >= max_left:
left + 1 右移到下一個位置
max_left = max(max_left,left位置的海拔高度)
answer += max_left - left位置的海拔高度
否則:
right - 1 左移到下一個位置
max_right = max(max_right,right位置的海拔高度)
answer += max_right - right位置的海拔高度
回傳 answer
C++
class Solution {
public:
int trap(vector<int>& height) {
int left = 0;
int right = height.size() - 1;
int left_max = height[left];
int right_max = height[right];
int answer = 0;
while (left < right){
if (left_max <= right_max){
left ++;
left_max = max(left_max,height[left]);
answer += left_max - height[left];
}
else{
right --;
right_max = max(right_max,height[right]);
answer += right_max - height[right];
}
}
return answer;
}
};